相对于传统砂轮,单层钎焊CBN砂轮在磨削航空航天钛合金、高温合金等难加工材料中显示出低磨削力、高加工效率等优势[1⁃2]。其根本原因是钎料合金与CBN磨粒、砂轮基体之间实现了高强度的化学结合,提高了砂轮基体对CBN磨粒的把持力[3]。目前,常见的钎焊方法主要包括真空炉中钎焊[4]、感应钎焊[5]以及激光钎焊[6]三种。其中,感应钎焊工艺具有钎焊周期短、低成本、可局部加热等特点,在单层钎焊CBN砂轮领域获得了广泛的应用和研究。研究表明,提高感应电流的频率,可以实现CBN砂轮的局部钎焊,从而有效减少钎焊热影响区,提高钎焊砂轮的精度[7]。然而,成型砂轮的感应钎焊一直是研究中的难点,其原因在于感应加热过程中的集肤效应和边缘效应[8]极容易引起横截面轮廓曲线复杂的成型砂轮表面温度分布不均匀,从而导致无法满足砂轮钎焊质量一致性的要求。
感应加热温度场的影响因素较多且规律复杂,国内外的相关研究以有限元数值仿真为主。例如Barka等[9]采用有限元法研究了齿轮表面感应淬火的温度场,发现电流强度和频率对齿根和齿顶的温度分布有重要的影响。高恺等[10]就平面的单回线感应加热问题进行了仿真研究,指出导磁体磁轭尺寸、电流频率以及电流强度等参数在合理的范围内能获得最佳加热效率和温度均匀性。童欣等[11]针对单层钎焊超硬磨料成型砂轮感应加热时存在的温度分布不均匀问题,借助有限元仿真软件在研究线圈与导磁体的结构尺寸对温度分布的影响规律的基础上,设计了感应器用于成型砂轮的钎焊。以上研究结果表明,感应电流和感应器结构是影响温度场的重要因素,但由于感应加热过程中材料物理属性的非线性特征,导致难以获得最佳工艺参数以及最优的感应器结构。
响应曲面法(response surface methodology,RSM)结合了数学方法和统计方法,专门用来研究响应值受多个变量影响进行建模与分析,最终优化该响应值[12⁃13]。该方法最早由Box和Wilson于1951年提出,随后在优化设计、可靠性分析等领域获得广泛应用。成型面感应加热温度场的控制属于典型多目标优化问题,目前RSM在感应加热领域已有不少研究报道。例如清华大学李峰等[14]针对平面单回线感应加热过程中的能量传递机理进行了研究,通过响应曲面法分析了影响温度精确性的工艺参数。Khalifa等[15]采用响应曲面法与人工神经网络结合的方法研究了齿轮表面感应淬火温度场的影响因素,最终准确预测了齿轮表面温度分布与淬火深度。这些研究结果表明RSM在感应加热过程中工艺参数优化等方面具有明显的优势。
本文基于RSM分析成型砂轮感应钎焊的温度分布的影响因素,以温度均匀度和平均温度为目标,建立2阶预测模型描述目标响应值与设计变量之间的关系,为研制高性能的单层钎焊成型砂轮奠定理论基础。
1 研究对象与方案设计
1.1 有限元模型
图1所示为用于钛合金叶片榫齿成型磨削的燕尾槽成型砂轮基体尺寸示意图,其材料为45钢。可以看出该砂轮工作面轮廓的曲率半径较小,分别为1.5 mm和1.6 mm,图中R为半径,为直径。
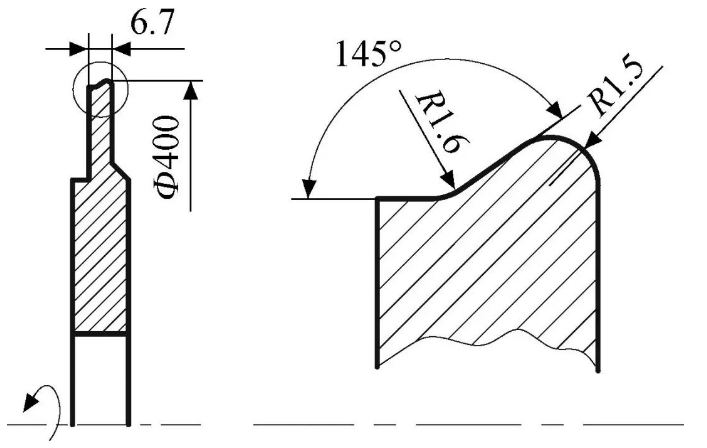
图1 燕尾槽成型砂轮基体尺寸示意图(单位:mm)
Fig.1 Geometry scheme of dovetail slot profiled grinding wheel matrix (unit:mm)
几何模型如图2(a)所示。考虑到模型的对称性,几何模型只有1/2。模型包括砂轮基体、紫铜管线圈、导磁体以及空气。需要指出的是,建模时将圆形砂轮基体简化为直工件,其高度为273 mm,用于等效砂轮的径向厚度。线圈横截面尺寸为2 mm×2.5 mm(实际加热过程中,紫铜管线圈中间有直径1 mm的孔,孔内部通入增压的冷却水),采用仿形结构,加热间隙(即与工件之间的距离)为h。导磁体为Ferritron 559H羰基铁,材料属性参见文献[16],其长度为L。
图2 有限元模型示意图
Fig.2 Scheme of finite element model
根据有限元计算原理,在线圈和工件的集肤深度内必须有至少2层网格才能保证计算精度,而这样会导致网格量巨大,影响效率。因此本文中,工件设置了表面阻抗边界条件[17]来避免较细的网格。另外,采用非网格化线圈来等效实际的线圈。在有限元计算时,该线圈不需要划分网格,仅需加载电流,电磁耦合采用Biot⁃Savart公式计算,收敛性较好[18]。上述简化处理能够在保证计算精度的前提下极大提高计算效率。最终网格总数约为5.8万,如图2(b)所示。
1.2 钎焊温度表征方法
温度均匀性对钎焊接头质量的一致性具有重要影响。为了合理地表征砂轮表面温度的均匀性,沿砂轮基体轮廓方向等间隔获取温度值,可得到温度序列Ti(i=1,2,…,n),如图3所示。本文中,沿砂轮基体轮廓线从点a到点b,间隔宽度为0.5 mm,共获得温度序列数n为55个。
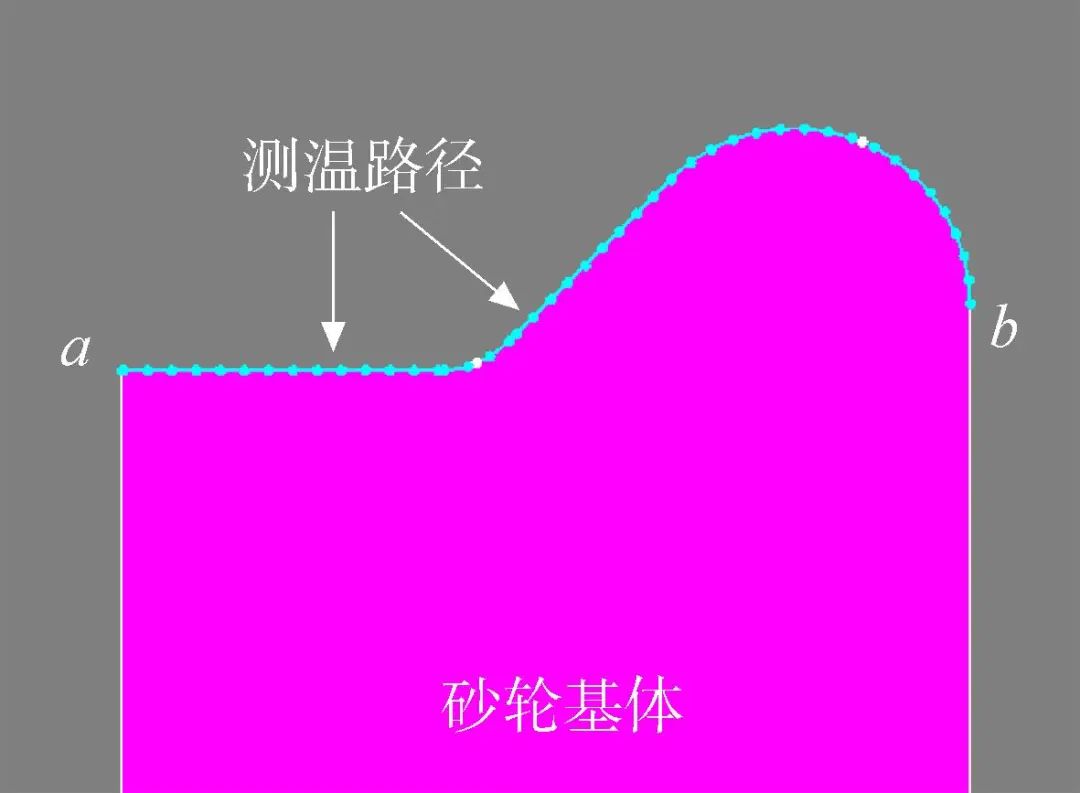
图3 成型面温度分析路径
Fig.3 Measured path for profiled surface temperature analysis
根据温度序列,可得到其均方差为
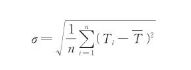
式中为平均温度,是温度序列的平均值。砂轮基体轮廓温度均匀度按下式定义:
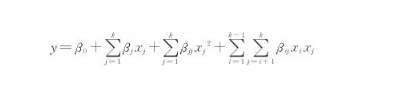
上述平均温度和温度均匀度U两个变量共同表征砂轮基体轮廓方向的温度均匀性。从式(2)可以看出,温度均匀度U等于100%时,意味着温度序列值都相等,即轮廓面上无温度差异。
1.3 Box⁃Behnken试验设计
选择感应电流I,导磁体长度L,加热间隙h作为设计变量,以平均温度和温度均匀度U为响应值,采用Design⁃Expert软件设计三因素三水平的仿真方案如表1所示,加热时间均为10 s。根据仿真结果,采用RSM建立的预测模型表达式为[15]
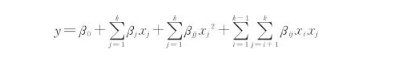
式中y为响应值;xj为第j个设计变量;k为设计变量的个数,本文中的设计变量为3个,即k=3;β0为常数,βj为第j线性系数,βjj为2阶偏移系数,βij为变量交互作用系数。

表1 响应曲面法各因素与水平
Table 1 Factor and level values of RSM
2 结果与讨论
2.1 温度均匀性的响应曲面分析
根据Box⁃Behnken方法设计的仿真结果如表2所示。从表中可以看出平均温度、温度均匀度两个变量与各设计因素之间不是线性关系。根据RSM,剔除非显著项,可分别获得平均温度和温度均匀度U两个响应值的预测模型为
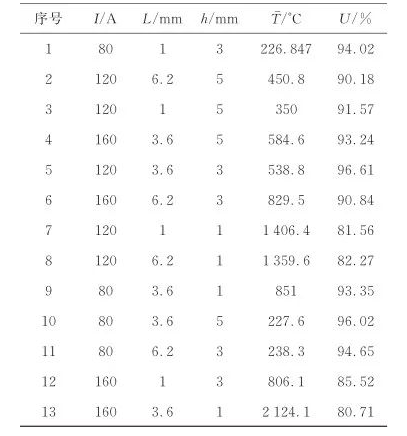
表2 各因素设计方案与仿真结果
Table 2 Design and simulation results of each factors

为了检验上述模型是否有效,对各系数进行方差分析(analysis of variance,ANOVA),结果分别如表3和表4所示。可以看到两个表中:决定系数R2均接近于1,说明拟合程度较好,且与调整决定系数Radj²接近,意味着建立的模型对拟合的数据做出了良好的调整;两个模型的P值(显著性检验)均小于0.000 1,表明模型极具有显著性[14];另外,根据表中F值(方差检验)可以得到各因素对响应值的影响大小,可以看出,三个因素对平均温度和温度均匀度U的影响的显著程度由大到小,依次为加热间隙h、感应电流I、导磁体长度L。式(4)中导磁体长度L仅在一次项中出现,且表3所示的方差分析表明该项的P值为0.626 5,P>0.05意味着该项的显著性比较低,因此RSM模型表明导磁体长度对平均温度的影响不显著。
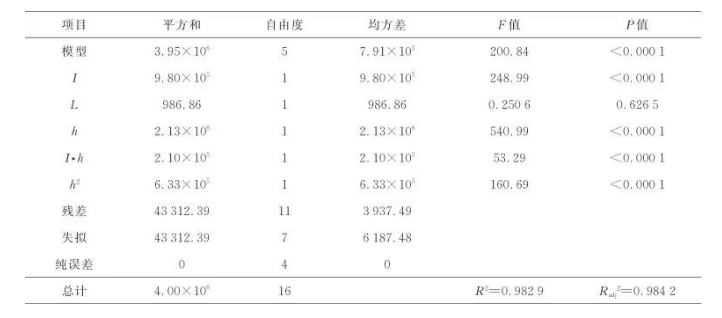
表3 平均温度的ANOVA结果
Table 3 ANOVA results of average temperature
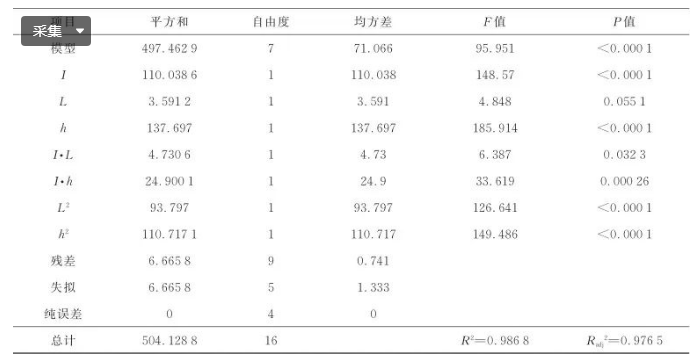
表4 温度均匀度的ANOVA结果
Table 4 ANOVA results of temperature uniformity
RSM不仅能够减少试验次数,还可以综合分析各因素交互作用下对响应值的影响。式(3)中的最后一项即表示因素间的交互作用[13]。从响应曲面模型式(4)、式(5)可知,平均温度的影响因素中,仅感应电流I和加热间隙h之间存在交互作用;而温度均匀度的影响因素中,存在两项交互作用,即感应电流I和导磁体长度L,感应电流I和加热间隙h。其他交互因素由于在响应曲面模型拟合过程中不显著,而被忽略剔除。
根据式(4),可以得到感应电流I和加热间隙h交互作用下,对平均温度的响应曲面如图4所示。从图中可以看出,随着感应电流的增加和加热间隙的减小,平均温度出现明显增大。另外,响应曲面在加热间隙坐标轴的方向斜率更大,说明相对于感应电流,加热间隙对平均温度的影响更加显著。响应曲面在底面的投影形成的等高线图的形状可反映因素间的交互作用,即椭圆形的等高线代表因素间的交互作用明显,而直线则表示因素间的交互作用不明显。图4可以看出感应电流与加热间隙整体的交互作用较少,仅在平均温度较低的时候存在一定的交互作用。
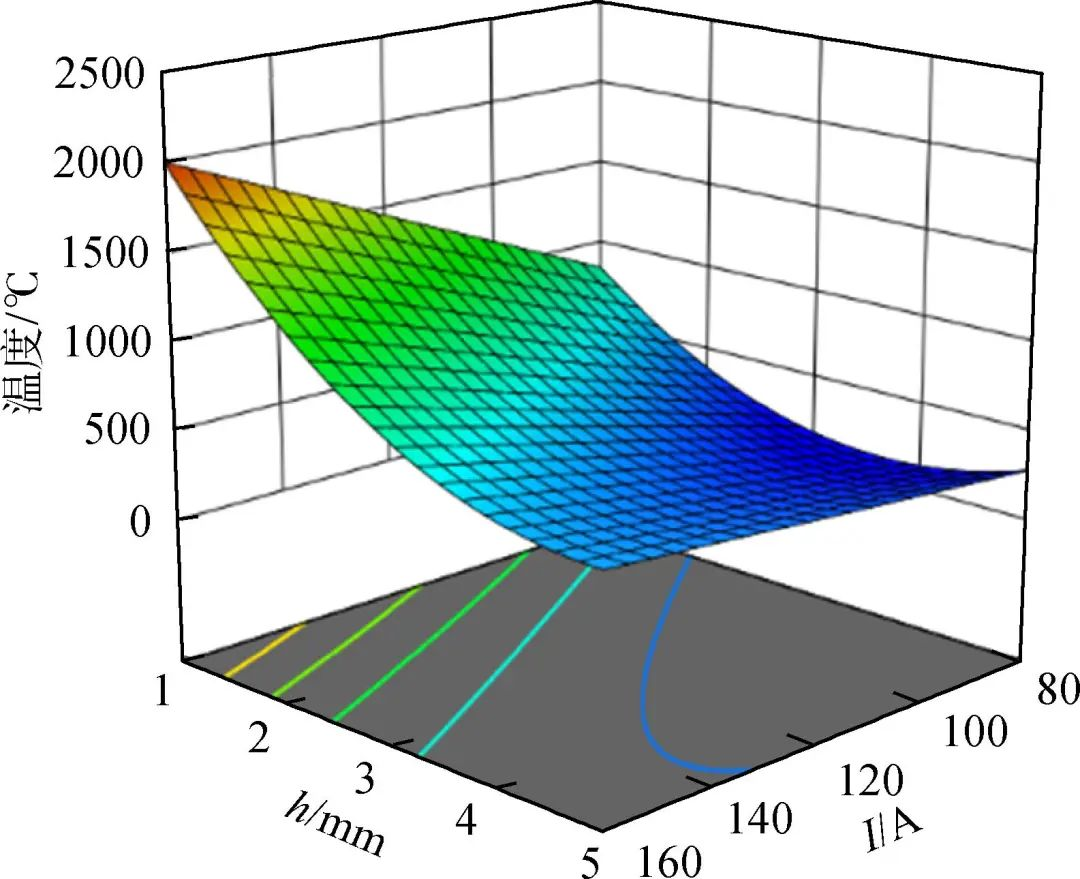
图4 感应电流和加热间隙对平均温度的交互作用
Fig.4 Interaction effect of induction current and heating gap on average temperature
各因素交互作用下对温度均匀度的响应曲面如图5所示。可以看出相对于平均温度,温度均匀度的非线性特征更加明显。随着感应电流的增加,温度均匀度呈下降趋势,而导磁体长度和加热间隙的增大,会导致温度均匀度先上升然后下降。从等高线图可以看出,感应电流与导磁体长度之间的交互作用最为显著,感应电流与加热间隙之间的交互作用次之。
图5 各因素对温度均匀度的交互作用
Fig.5 Interaction effect of factors on temperature uniformity
大量研究结果显示,导磁体作为一种磁场强化手段,可有效约束局部的磁力线分布,从而提高感应加热的效率[9,19]。本文中,仿形线圈在成型面凸出区域的加热效率高,而在内凹区域的加热效率低,从而导致型面轮廓方向温差较大。仿真中导磁体长度的最大值为6.2 mm,仅作用在成型面内凹的局部区域,因此其主要作用是提高成型面内凹区域的加热效率,从而减少整个型面的温差。图6所示为导磁体对成型砂轮表面温度场的影响。从图中可以看出无导磁体时,型面内凹处和凸出部分的温差比较大,分别为682.9 ℃和916.7 ℃。有导磁体之后,型面温差明显减小,其中内凹处的温度提高到791.2 ℃,而凸出部分的温度变化不明显,为922.5 ℃。可见,本文条件下导磁体对平均温度的影响不明显,而对温度均匀度的影响十分显著。
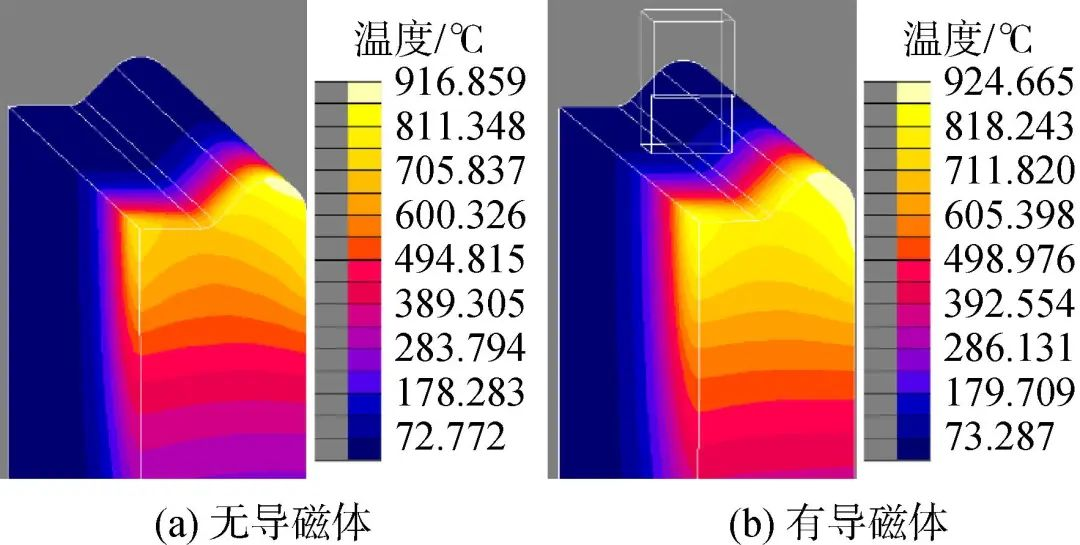
图6 导磁体对温度场的影响
Fig.6 Effect of magnetizer on temperature field
2.2 感应线圈优化与试验验证
前期研究表明Ag⁃Cu⁃Ti钎料感应钎焊CBN砂轮的最佳钎焊温度为940 ℃[5],因此,感应线圈的优化目标是平均温度为940 ℃,温度均匀度U为最大化。三个因素中,加热间隙对温度均匀性的影响最为显著。另一方面,考虑到加热间隙太小会导致在实际钎焊过程中线圈与CBN磨粒接触,因此增加了一个约束条件即加热间隙h=2 mm。基于相应曲面模型,可获得最优参数为I=124.4 A,L=3.8 mm。此时预测模型得到的平均温度=940 ℃,温度均匀度U=91.96%。为了验证该最优化方案的效果,搭建了如图7(a)所示的试验装置。图中感应线圈导磁体长度为3.8 mm,加热间隙为2 mm,感应电流为124.4 A。采用德国OPTRIS PI230型红外热像仪进行实时测温,其发射率设置为0.8。图7(b)所示为加热时间为10 s时刻工件轮廓表面的温度分布测量值与仿真结果对比。可以看出,仿真结果显示工件轮廓测量路径上的温度范围为906.8~1 029.8 ℃,平均温度为959.6 ℃,温度均匀度为95.41%.而试验获得的温度范围整体偏低,为903.8~952.7 ℃,平均温度为924.1 ℃,而温度均匀度达到了98.34%,与响应曲面预测模型的误差分别为1.69%和6.94%。从图中还可以看出,温度的试验测量值与仿真结果之间的误差最大值为8.75%。造成上述误差的主要原因可能是有限元模型采用了一定的简化处理,如工件的表面阻抗边界条件以及非网格化线圈等,从而导致了仿真结果的误差。尽管如此,上述结果仍然可以证明仿真模型具有一定的准确性和可靠性。
图7 感应钎焊温度均匀性优化结果的验证
Fig.7 Veryfication of optimal results of temperature uniformity in induction brazing
此外,从图7(b)还可以看出,试验条件下,工件凸出部位的温度分布明显低于仿真结果,误差相对较大。可能的原因是试验条件下,受实际工艺的限制,线圈与工件之间的相对位置存在一定的偏差,导致实际的加热间隙比设定值稍大。而从温度均匀性的相应曲面分析结果可知,加热间隙h对砂轮表面的温度影响最为显著,导致工件表面的实际加热温度比仿真结果更低。
2.3 高频感应钎焊成型CBN砂轮试验
待钎焊的成型砂轮采用无镀膜CBN磨粒,平均直径为150~180 μm。钎料为Ag⁃Cu⁃Ti合金粉末,主要组分为96(72Ag⁃28Cu)⁃4Ti(质量分数,%),熔点为880 ℃。高频感应钎焊参数基于优化结果,即与文中第2.2节的试验参数相同。砂轮钎焊原理与钎焊装置如图8(a)所示。钎焊时,采用开放式的局部Ar气保护,Ar气体积流量为40 L/min。
图8 高频感应钎焊成型CBN砂轮
Fig.8 High frequency induction brazing of profiled CBN grinding wheel
钎焊CBN砂轮形貌照片如图8(b)所示。可以看出钎料在成型面各处的铺展性比较均匀,表明钎焊过程中在成型面的温度分布具有较好的均匀性。
3 结 论
1) 提出了基于平均温度和温度均匀度的成型砂轮感应钎焊温度均匀性表征模型,并采用有限元仿真分析结果获得了成型面平均温度和温度均匀度的2阶响应曲面预测模型,模型拟合程度良好,可用于平均温度和温度均匀度的预测。
2) 基于预测模型和方差分析,各因素对平均温度和温度均匀度影响的显著程度从大到小依次为加热间隙h、感应电流I、导磁体长度L。
3) 基于响应曲面法优化线圈结构和工艺参数,开展了感应加热试验,结果显示成型面平均温度为924.1 ℃,温度均匀度为98.34%,与响应曲面预测模型的误差分别为1.69%和6.94%。
4) 高频感应钎焊成型CBN砂轮宏观形貌显示,钎料在成型面各处铺展的一致性好,表明钎焊过程中在成型面的温度分布具有较好的均匀性。
作者简介:李奇林(1984-),男,副教授、硕士生导师,博士,主要从事超硬磨料砂轮钎焊技术研究。
通讯作者:王西超(1982-),男,讲师、硕士生导师,博士,主要从事人工智能与数学建模研究。E‑mail:wangxc@sdju.edu.cn
基金信息: 国家自然科学基金(51905234,51805231)
中图分类号: V263.1; TG454
文章编号:1000-8055(2022)09-1915-08
文献标识码: A
收稿日期:2022-01-23
出版日期:2022-09-28
网刊发布日期:2022-10-08
本文编辑:秦理曼


 手机资讯
手机资讯 官方微信
官方微信









 豫公网安备41019702003645号
豫公网安备41019702003645号